solidworks草图 样式样条曲线 详细介绍|SW贝塞尔曲线基础教程

您可以将样式样条曲线绘制为两个现有实体之间的桥接曲线。文章源自 solidworks教程网 http://gocae.comsolidworks教程网-http://gocae.com/1694.html

要绘制样式样条曲线草图：文章源自 solidworks教程网 http://gocae.comsolidworks教程网-http://gocae.com/1694.html

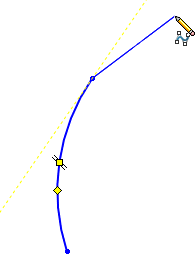绘制两个圆弧实体的草图。文章源自 solidworks教程网 http://gocae.comsolidworks教程网-http://gocae.com/1694.html

将指针悬停在推理线上，并单击以添加第二个控制顶点，如图所示。文章源自 solidworks教程网 http://gocae.com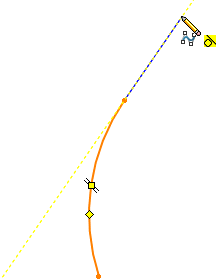solidworks教程网-http://gocae.com/1694.html

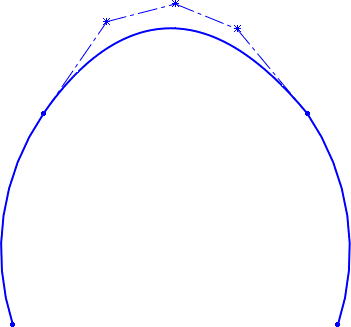
继续向右移动指针，并将其悬停在下一条推理线上。 如果您将第三个控制顶点捕捉至推理线，则端点处将生成相等曲率几何关系。文章源自 solidworks教程网 http://gocae.com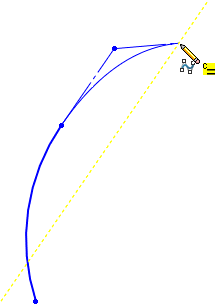solidworks教程网-http://gocae.com/1694.html

要完成绘制样式样条曲线，请继续添加更多控制顶点。 当您到达第二个圆弧的端点时，按 ALT 并双击端点。

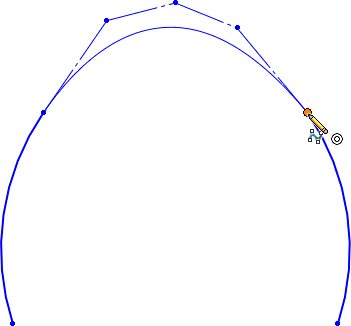
按 ALT 可应用上一个控制顶点处的自动相切几何关系。

2. 插入控制顶点

插入控制顶点命令可以为样式样条曲线添加一个或多个控制顶点。 您添加的每个控制顶点都会增加曲线度。

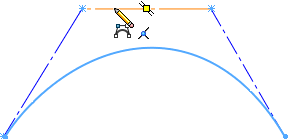
1. 右键单击控制多边形的任意位置 > 选择 插入控制顶点  > 单击多边形线段插入控制点  

 

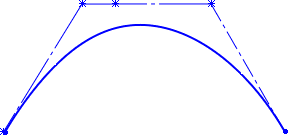
3. 贝塞尔曲线基本概要

维基百科上有很赞但不推荐细看的Gif动画，以下动图都是基于数学公式

3.1 一阶贝塞尔（直线）

一阶贝赛尔曲线上的由两个点确定 P0 和P1,当t在0--->1区间上递增时，根据
此会得到多个点的坐标，其实这些的点就是一条直线上的点。

1. B(t) = P0 + (P1-P0)*t
2. B(t) = (1-t)P0 + tP1
3. //=>
4. B(t).x = (1-t)P0.x + tP1.x
5. B(t).y = (1-t)P0.y + tP1.y

线性贝塞尔曲线演示动画，t在[0,1]区间

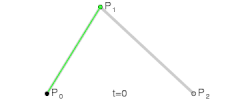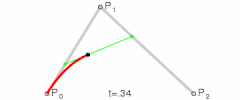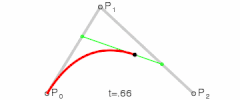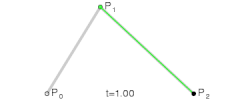
3.2 二阶贝塞尔（曲线）

二阶贝赛尔曲线由`3`个点确定，它可以理解成是这样的一阶贝赛尔曲线：确定该`一阶贝赛尔曲线`的两个点是变化的。

这两个点（设分别为Pm,Pn）是怎样变化的呢，这两个点又分别是(P0,P1)确定的`一阶贝赛尔曲线`和(P1,P2)确定的`一阶贝赛尔`曲线上的点。

于是有了2阶贝赛尔曲线的公式

1. Pm(t) = (1-t)P0 + tP1
2. Pn(t) = (1-t)P1 + tP2
3. B(t) = (1-t)P_m(t) + tP_n(t) = (1-t)² P₀ + 2t(1-t)P₁+ t²P₂

二次贝塞尔曲线演示动画，t在[0,1]区间